Я недавно нашёл прекрасный пост Gary Weissman’а Grey’s Anatomy Network of Sexual Relations (перевод на русский тут) и вдохновился им. Для тех, кто ничего не слышал об этом телесериале, сообщаю, что он чрезвычайно популярен, отмечен наградами как лучшая медицинская драма, транслируемая ABC. Идя навстречу ожиданиям зрителей, шоу регулярно показывает, как его герои флиртуют друг с другом.
Пытаясь дать студентам-медикам ряд простейших концепций анализа социальных сетей, Weissman создал набор сетевых данных о сексуальных контактах героев этого сериала. Хотя я особо не интересуюсь ни этим шоу, а сексуальные или воображаемые сети лежат вдали от моих исследовательских интересов, пост Weissman’а мне кажется отличной демонстрацией анализа социальных сетей в педагогических целях.
Я бы хотел, ради развлечения, вернуться к этим данным и рассмотреть их с помощью экспоненциального моделирования случайных графов (ERGM) в аспекте образования связей. Прежде чем я продолжу, я бы хотел сказать, что самые лучшие пособия по ERGM созданы их авторами и доступны на сайте. Моим любимым пособием из-за его прикладной направленности является серия презентаций на февральской конференции Sunbelt Workshop 2011 г. Если вы всерьёз настроены изучить ERGM, то указанные публикации должны стать вашими настольными книгами. Тем не менее, я думаю, что существует та аудитория, которая с бОльшим восторгом наблюдает за приключениями сексуальных врачей на телевидении, чем читает о брачных сетях во Флоренции 16 века.
Экспоненциальные модели случайных графов являются способом понять процесс возникновения сетевой структуры, процесс образования в ней сетей. В нашем примере «образование сетей» и «снять потрахаться» являются синонимами. Эти модели работают, измеряя некий набор известных сетевых характеристик и используя распределение их значений для генерации случайных сетей. Такие случайные сети затем сравниваются с сетью наблюдаемой, чтобы оценить правдоподобие модели. Хорошие ERG-модели продуцируют сети, изоморфно похожие на наблюдаемую сеть, и пользуются небольшим набором характеристик. Плохие ERG-модели продуцируют сети, которые слабо похожи на наблюдаемую сеть, но при этом используется много ненужных характеристик.
Какими характеристикам следует пользоваться? Число рёбер (т. е. «связей», «отношений») является одной из самых важных. Если мы занимаемся образованием связи, то очень важно знать число этих связей. Кроме того, в посте Weissman’а некоторые комментаторы упоминали важность пола персонажей или, к примеру, их должность в больнице. Узлы (т. е., «акторы», «вершины») могут иногда характеризоваться атрибутами, такими как пол, возраст, должность или астрологический знак. При моделировании сети можно использовать атрибуты узлов, чтобы оценить такие ассортативные эффекты как общая гомофилия («Спят ли члены больничных коллективов с сотрудниками, занимающими такие же должности?»), дифференциальная гомофилия («Спят ли штатные врачи с другими такими же? Делают ли они это чаще, чем интерны с другими интернами?») и ассортативное смешивание («Do resident-attending couples occur more frequently than we’d expect vis-à-vis nurse-attending couples?»). Можно анализировать и другие свойства сетей, но это зависит от доступности данных, типа анализируемой сети (направленная, ненаправленная, бимодальная), а также от сходимости модели.
Использованные здесь данные восходят к тем, которые Weissman сделал доступными. Я добавил узлы и рёбра по информации, найденной при просмотре Wikipedia. Я включал лишь те персонажи, которые переспали с одним или несколькими другими персонажами в сериале. Я также добавил такие атрибуты, как пол персонажа, расу, должность в больнице, приблизительный возраст, номер сезона, в котором он появился, и астрологический знак, под которым родился актёр. Я собрал эти атрибуты из Wikipedia и IMDB. Для простоты я кодировал расу каждого персонажа как чёрный (black), белый (white) или другой (other). Хотя я не люблю рассматривать расу именно в этих терминах, однако число персонажей и их разнообразие невелико, чтобы вдаваться в нюансы этого вопроса. Что касается приблизительного возраста персонажей, то я пользовался возрастом актёров, их играющих, а в двух случаях мне пришлось самому сделать предположения. Как у Weissman’а, нынешние данные, вероятно, не содержат какой-то информации об отношениях, узлах, упрощают описание персонажей и их взаимоотношений.
Для начала откройте R-терминал. Установите и загрузите пакеты
ergm и RCurl, если вы не сделали этого раньше.install.packages("RCurl"); install.packages("ergm")
library(RCurl); library(ergm)Пакет
RCurl будет использован для того, чтобы загрузить данные из моего файла на Google Docs. Пакет ergm включает несколько других пакетов, таких как network, поскольку ERGM использует объекты, созданные последним.Далее, прочтите данные и создайте объект класса
network.#First, read in the sociomatrix
ga.mat<-getURL("https://docs.google.com/spreadsheet/pub?key=0Ai--oOZQWBHSdDE3Ynp2cThMamg1b0VhbEs0al9zV0E&single=true&gid=0&output=txt",ssl.verifypeer = FALSE)ga.mat<-as.matrix(read.table(textConnection(ga.mat), sep="\t",header=T, row.names=1, quote="\""))#Second, read in the network attributes
ga.atts<-getURL("https://docs.google.com/spreadsheet/pub?key=0Ai--oOZQWBHSdDE3Ynp2cThMamg1b0VhbEs0al9zV0E&single=true&gid=1&output=txt",ssl.verifypeer=FALSE)ga.atts<-read.table(textConnection(ga.atts), sep="\t", header=T, quote="\"",stringsAsFactors=F, strip.white=T, as.is=T)#Third, create a network object using the sociomatrix and its corresponding attributes
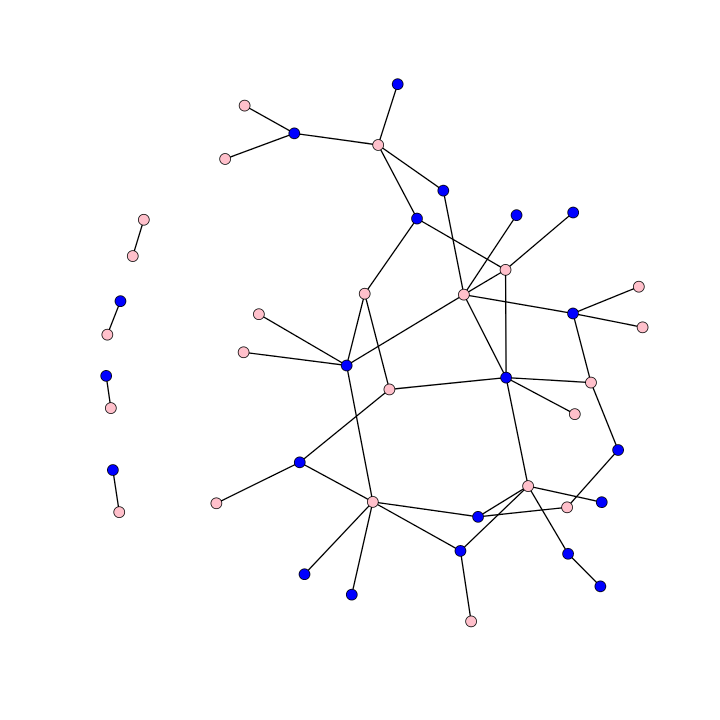
ga.net<-network(ga.mat,vertex.attr=ga.atts,vertex.attrnames=colnames(ga.atts),directed=F,hyper=F,loops=F,multiple=F,bipartite=F)Теперь, когда вы получили данные, мы можем поиграть с ними. Прежде чем перейти к моделированию, давайте посмотрим на схему сети, отметив розовым цветом узлы, означающие женщин, и голубым — мужчин.
plot(ga.net,vertex.col=c("blue","pink")[1+(get.vertex.attribute(ga.net,"sex")=="F")],label=get.vertex.attribute(ga.net,"name"), label.cex=.75)Расположение узлов на вашем рисунке может несколько отличаться. Здесь то, что получилось у меня:
Следует отметить несколько интересных особенностей этой сети.
Во-1, с точки зрения связности у нас есть большой связный компонент,но в целом граф поделён на четыре отдельных компонента. Если бы шоу продолжалось без появления новых персонажей, я бы думал, что один из самых маленьких компонентов должен бы «соединиться» с самым большим компонентом.
Во-2, большая часть сексуальных отношений в сериале суть гетеросексуальны. Только два ребра (torres-arizona и torres-hahn) были однополыми. По всей видимости, здесь нет нечётно-численных циклов: в сексуальных сетях циклы из трёх, пяти, семи и др. элементов содержат как минимум одну однополую связь внутри цикла.
В-3, в отражение способа построения выборки сеть не содержит сексуально-одиноких изолятов. Минимальная степень (число связей, падающих на узел) равна единице. В-четвёртых, сеть оказывается уязвимой перед табу «бывший бывшей бывшего». В одном из исследований сексуальных сетей учёные обнаружили запрет на создание пары с бывшим партнёром бывшего партнёра бывшего партнёра из-за возможных осложнений. Кажется, что здесь есть как минимум три цикла, отвечающих критериям этого табу. Вместе с тем, также хорошо известно, что нежелательные последствия, возникающие от сексуальных отношений с другими, делают шоу правдоподобным.
Давайте начнём наш формальный анализ с базовой модели, которая включает только число рёбер и, как второй предиктор,
nodematch("sex"), который схватывает гетеросексуальную тенденцию сети.ga.base<-ergm(ga.net~edges+nodematch("sex")) #Estimate the model summary(ga.base) #Summarize the modelВот выдача команды
summary(ga.base): ==========================
Summary of model fit
==========================
Formula: ga.net ~ edges + nodematch(“sex”)
Iterations: 20
Monte Carlo MLE Results:
Estimate Std. Error MCMC % p-value
edges -2.3003 0.1581 NA <1e
-04="-04" -3.1399="-3.1399" 0.001="0.001" 0.01="0.01" 0.05="0.05" 0.1="0.1" 0.7260="0.7260" 0="0" 1311.43="1311.43" 1="1" 2="2" 320.47="320.47" 324.47="324.47" 334.17="334.17" 944="944" 946="946" 990.97="990.97" aic:="aic:" bic:="bic:" code="code" codes:="codes:" degrees="degrees" deviance:="deviance:" e-04="e-04" freedom="freedom" na="na" nodematch.sex="nodematch.sex" null="null" of="of" on="on" residual="residual" signif.="signif."В согласии с ожиданиями число рёбер и гетеросексуальность суть значимые предикторы образования связей, поскольку p-значение существенно меньше, чем условный уровень значимости 0.05. Колонка «MCMC%» слева указана как пропущенная (NA), поскольку эта модель не требует оценки марковских цепей по методу Монте-Карло. Коэффициенты, −2.30 и −3.14, показывают условные логарифмы шансов (log-odds), таким образом логарифмы шансов того, что два персонажа вступили в сексуальные отношения, равны (-2.30)*увеличение числа связей на единицу + (-3.14)*увеличение числа однополых отношений. Логарифм шансов того, что одна гетеросексуальная связь образуется внутри сети, равен −2.30, что даёт её вероятность exp(-2.30)/(1+exp(-2.30)) = 0.09. Аналогично, логарифм шанса образования гомосексуальной связиравен −2.30-3.14 = 5.44, что соответствует вероятности 0.004 = exp(-5.44)/(1+exp(-5.44)).
Давайте посмотрим, какую случайную, расчётную сеть эта модель могла бы создать.
plot(simulate(ga.base),vertex.col=c("blue","pink")[1+(get.vertex.attribute(ga.net,"sex")=="F")])Ваша картинка может несколько отличаться от того, что получилось у меня:
Эта сеть точно отражает как число рёбер, так и склонность к образованию гетеросексуальных связей, однако здесь не всё в порядке: некоторые из наших узлов суть изоляты. Иными словами, расчёт предсказывает существование в сети сексуально-воздерживающихся индивидов. Поскольку никаких таких людей в нашей реальной сети нет из-за особенностей формирования выборки, построенная модель неудовлетворительна.
Хотя у нас есть значения критерия согласия (goodness of fit), данного функцией правдоподобия, один обычный, систематический способ определения критерия согласия — это сравнение параметров немоделированной, наблюдаемой сети с такими же параметрами рассчитанных ERGM сетей.
ga.base.gof<-gof(ga.base) summary(ga.base.gof) #Summarize the goodness of fit par(mfrow=c(3,1)); plot(ga.base.gof) #Plot three windows. It's OK to ignore the warning.Рисунок воспризводит ту же информацию, которую выдаёт команда
summary(). p-Значения в правых колонках суть вероятности того, что рассчитанные сети точно совпадают с сетью наблюдаемой в ряду данных параметров. Мы видим, что в терминах of the edgewise shared partner and minimum geodesic distance measurements represent the data quite well. Однако, если мы посмотрим на такой параметр как центральность, то увидим то, что согласуется с нашими выводами из рисунков — число воздерживающихся изолятов (узлов с центральностью 0) больше, чем нужно, число узлов с центральностью 1 (моногамистов) — меньше, и что нет оценок для узлов с центральностью 3 и 9.Мы сейчас добавим в модель параметр, контролирующий эффект моногамии (центральность 1).
ga.base.d1<-ergm(ga.net~edges+nodematch("sex")+degree(1)) summary(ga.base.d1) plot(simulate(ga.base.d1),vertex.col=c("blue","pink")[1+(get.vertex.attribute(ga.net,"sex")=="F")]) ga.base.d1.gof<-gof(ga.base.d1); summary(ga.base.d1.gof) par(mfrow=c(3,1)); plot(ga.base.d1.gof)Если принять значение BIC предыдущей модели 334.17 как исходное, то мы увидим, что модель ga.base.d1 лучше — её BIC равен 316.56. Эффект моногамии также является статистически значимым. Рисунок демонстрирует меньше изолятов, что подтверждает команда
gof(). Судя по значениям критерия согласия, модель кажется разумным приближением к реальности, если не принимать во внимание персонаж шоу с девятью сексуальными партнёрами.В отличие от предыдущей модели, эта использует методику оценки марковских цепей (MCMC). Мы можем оценить результаты MCMC.
mcmc.diagnostics(ga.base.d1)В выводе следует сначала глянуть на второй пункт, в котором сравниваются параметры расчётной и наблюдаемой моделей.
Are sample statistics significantly different from observed?
edges nodematch.sex degree1 Overall (Chi^2)
diff. -0.0968000 0.0232000 0.0534000 NA
test stat. -0.2942081 0.8328180 0.3379779 1.086016
P-val. 0.7685989 0.4049474 0.7353798 0.780451Вроде бы всё в порядке: рассчитанные при помощи MCMC графы значимо не отличаются от наблюдаемого. Давайте посмотрим по-другому:
Sample statistics auto-correlation:
Chain 1
edges nodematch.sex degree1
Lag 0 1.0000000 1.00000000 1.0000000
Lag 100 0.8476292 0.47956824 0.7334256
Lag 200 0.7332856 0.26641687 0.6116231
Lag 300 0.6371281 0.17109432 0.5198955
Lag 400 0.5587029 0.12489565 0.4480439
Lag 500 0.4883954 0.08496445 0.3860807
Sample statistics burn-in diagnostic (Geweke):
Chain 1
Fraction in 1st window = 0.1
Fraction in 2nd window = 0.5
edges nodematch.sex degree1
-1.590 -1.068 1.372
P-values (lower = worse):
edges nodematch.sex degree1
0.1117691 0.2856841 0.1701817 В целом, нет ничего подозрительного в результатах диагностики MCMC. Параметр автокорелляции между лагами несколько больше, чем предпочитаемый мною (лаги должны быть ближе к нулю и дальше от единицы, за исключением нулевого лага). Кроме того, статистика Geweke, приблизительно соответствующая z-статистике, когда её p-значения незначимы, должна быть значительно ближе к нулю. К счастью, мы можем так изменить некоторые параметры по умолчанию в MCMC для того, чтобы получить более приемлемый результат.
ga.base.d1<-ergm(ga.net~edges+nodematch("sex")+degree(1),control=control.ergm(MCMC.burnin=50000, MCMC.interval=5000))При увеличении MCMC.burnin с 10,000 (по умолчанию) до 50,000 должен уменьшаться параметр Geweke. При увеличении MCMC.interval со 100 (по умолчанию) до 5000 должна уменьшаться автокорреляция между лагами. Если бы параметры нашего расчётного образца действительно значимо отличались от наблюдаемых, мы бы увеличили размер выборки в MCMC с 10,000 (по умолчанию) до 20,000 или даже 50,000.
ga.base.d1<-ergm(ga.net~edges+nodematch("sex")+degree(1),control=control.ergm(MCMC.burnin=50000,MCMC.interval=5000, MCMC.samplesize=50000))Нам следовало бы поупражняться в увеличении этих параметров MCMC, но это может резко увеличить время расчётов.
summary(ga.base.d1) #The figures are mostly the samemcmc.diagnostics(ga.base.d1)Ура! MCMC диагностика заметно улучшилась, что указывает на большую жёсткость нашей последней модели.
Теперь, когда мы понимаем чуть больше, как оценивать качество модели, мы можем вернуться к интригующему вопросу секса! Только что мы моделировали сеть по числу рёбер, склонности к гетеросексуальности и по моногамии, но могут ли другие аспекты привнести смысл в анализ? Я бы предложил начать с возраста, поскольку большинство любовных связей возникают между сверстниками.
ga.base.d1.age<-ergm(ga.net~edges+nodematch("sex")+degree(1)+absdiff("birthyear"),control=control.ergm(MCMC.burnin=50000, MCMC.interval=5000))summary(ga.base.d1.age)mcmc.diagnostics(ga.base.d1.age)summary(gof(ga.base.d1.age))Кажется, модель ощутимо улучшилась! Значение BIC снизилось с 316.56 до 297.51,
Наконец, давайте рассмотрим ассортативность с точки зрения группировки по расам. Предыдущие исследования юношеских сексуальных и любовных сетей открыли такую ассортативность. Создательница сериала, Shonda Rhimes, сознательно построила отбор актёров так, чтобы представить расовое разнообразие. Поскольку шоу включает ряд афроамериканских (наряду с обилием других не-белых) персонажей, можно попытаться установить, привело ли такое разнообразие при отборе персонажей к расовому разнообразию в сексуальных отношениях. Для начала, давайте попробуем построить модель общей гомофилии по расе.
ga.base.d1.age.race<-ergm(ga.net~edges+nodematch("sex")+degree(1)+absdiff("birthyear")+nodematch("race"),control=control.ergm(MCMC.burnin=50000,MCMC.interval=5000))summary(ga.base.d1.age.race)mcmc.diagnostics(ga.base.d1.age.race)summary(gof(ga.base.d1.age.race))Мы в самом деле нашли эффект расового отбора, предполагающий, что образование связи более вероятно между персонажами одной и той же расы. В этом шоу сексуальные отношения являются скорее внутри-, нежели межрасовыми по сравнению с тем, что было бы, если бы персонажи разных рас комбинировались совершенно случайно.
Но возможно, что белые персонажи проявляют большую гомофилию, а чёрные — меньшую? Или наоборот? Мы можем посмотреть на это как на дифференциальную гомофилию. В модель добавляем параметр
diff=T к слагаемому nodematch("races").ga.base.d1.age.racediff<-ergm(ga.net ~ edges + nodematch("sex") + degree(1)
+absdiff("birthyear") + nodematch("race", diff=T), control=control.ergm(MCMC.burnin=50000,MCMC.interval=5000))summary(ga.base.d1.age.racediff)Хотя мы можем моделировать дифференциальную гомофилию,
ergm() не смог интерпретировать категорию «other», поскольку в наблюдаемой сети нет сексуальных отношений между латиноамериканцами и азиатоамериканцами. ergm() указывает на эту сложность следующей фразой: Observed statistic(s) nodematch.race.Other are at their smallest attainable values. Their coefficients will be fixed at -Inf.Аналогично, the AIC, BIC, отклонение и эффекты nodematch.race.Other помечены как NA в summary. Давайте попробуем создать новую модель, исключив гомофилию между латиноамериканцами и азиатоамериканцами. Чтобы это сделать, мы включаем параметр
keep=c(1,3) в слагаемое nodematch("race"), поскольку «Black» и «White» были первой и третьей категориями, перечисленными в summary(ga.base.d1.age.racediff).ga.base.d1.age.racediff<-ergm(ga.net~edges+nodematch("sex")+degree(1)+absdiff("birthyear")+nodematch("race", diff=T, keep=c(1,3)),control=control.ergm(MCMC.burnin=50000, MCMC.interval=5000))summary(ga.base.d1.age.racediff)mcmc.diagnostics(ga.base.d1.age.racediff)summary(gof(ga.base.d1.age.racediff))Как и в предыдущей модели, мы видим значимую ассортативность по расовым группам в сериале. Как чёрные, так и белые персонажи проявляют склонность к расовой гомофилии бОльшую, чем можно было бы ждать, если бы выбор партнёра был случайным. Эта модель также указывает, что эффекты гомофилии сильнее среди афроамериканских персонажей (на это указывает более высокий коэффициент и меньшее p-значение при nodematch.race.Black по сравнению с nodematch.race.White term). Проверка
Давайте посмотрим на картинку.
plot(simulate(ga.base.d1.age.racediff),vertex.col=c("blue","pink")[1+(get.vertex.attribute(ga.net,"sex")=="F")])Ваша может выглядеть несколько иначе, но в целом, кажется, эта модель воспроизводит оригинальные данные достаточно хорошо. Результат расчётов отличается наличием большого компонента, небольшим количеством изолятов (их даже может не быть), несколькими небольшими компонентами и, хотя отношения на ней преимущественно гетеросексуальны, мы видим четыре однополых связи (в оригинальных данных их было две).
Хотя число съёмов в сериале Grey’s Anatomy может казаться удивительным, в аспекте образования диад видно скорее традиционное восприятие сексуальных отношений: доминируют нормы моногамии, а бОльшая часть связей суть гетеросексуальны и соединяют пары близкого возраста и одной расы. Следует, однако отметить, что описанный анализ обошёл ряд альтернативных версий, которые могли бы лучше отразить свойства сети. Я приглашаю читателей самостоятельно поиграть с данными и с другими моделями. Несколько дополнительных примеров:
#Perhaps men and women have different tendencies to form sexual partnerships?
ga.base.d1.age.sex<-ergm(ga.net~edges+nodematch("sex")+degree(1)
+absdiff("birthyear")+nodefactor("sex"),
control=control.ergm(MCMC.burnin=100000, MCMC.interval=5000))
#Maybe less "traditional" than previously concluded?#Perhaps you're interested in the assortative mixture among roles in the hospital?
#Resident-resident sexual contacts (28) are the reference group,
#and unobserved pairings between positions (3-5, 9, 12-15, 17-21, 24, 27) are omitted.
ga.base.d1.age.rolemix<-ergm(ga.net~edges+nodematch("sex")+degree(1)+absdiff("birthyear")
+nodemix("position", base=c(3:5, 9, 12:15, 17:21, 24, 27, 28)),
control=control.ergm(MCMC.burnin=50000, MCMC.interval=5000))list.vertex.attributes(ga.net) #List the different vertex attributes in the network objectget.vertex.attribute(ga.net, "sign") #Provides each actor's astrological sign.?ergm.terms #This command will provide a list of other terms that ergm() can model
?control.ergm #This command will present different options on the estimation methods.


Немає коментарів:
Дописати коментар